馬場適性について

ウイニングポストには
芝への適性の高さ、ダートへの適性の高さを表すために
馬場適性というものが存在する。

◎＞〇＞△＞×の順で
適性が高いという表現であるが、

この適性の違いによって

• どれほど着順に差が生じるのか
• 各適性間の差はスピードに置き換えるとどれほどなのか

カスタムレースを用いて調査する。

調査条件

ベースは同じ競走馬で
スピード70（B相当）
サブパラB
脚質：自在　気性：普通　性格：普通

馬場適性のみ変更した４種類の架空馬を用意。

カスタムレースで

東京芝2000ｍ（良）
枠順ランダム

各種４頭の計16頭で走ってもらい、
それぞれの平均着順を調査する。

適性毎の平均着順

能力が同じであり、適性のみ◎○△×４種類バラバラの競走馬達に
東京芝2000ｍを20回走ってもらった結果、
以下の通りとなった。

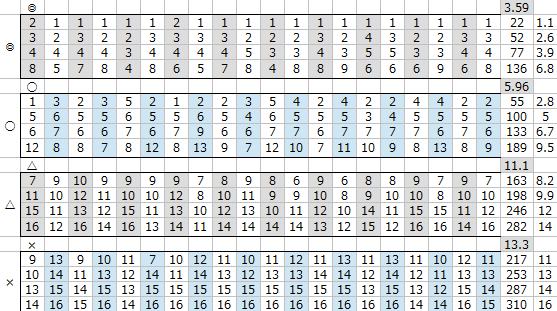
適性が高いほど平均着順が良く、
適性○であっても適性◎を相手に１着を取るなど奮戦しているが
適性△以下は振るわないことがわかる。

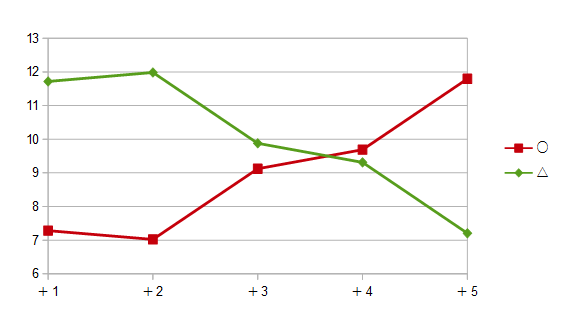
この表を見やすくグラフ化したものが以下である。

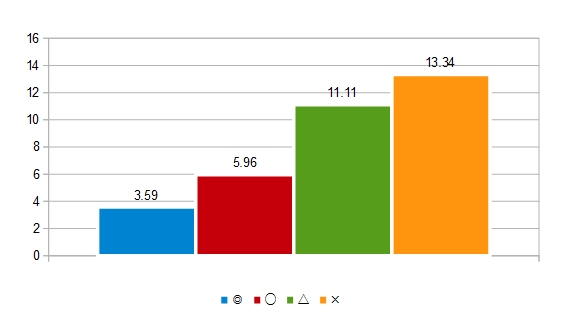
◎と○の差はおおよそ2.4
〇と△の差はおおよそ5.1
△と×の差はおおよそ2.2

◎と○、△と×の間はほぼ同じであるが、
〇と△の差は他の２倍ほどの開きがある。

今度はこの各適性間のスピード差を確認する。

適性間のスピード差

◎と○のスピード差

◎と○の差をスピードのみで埋めるためにどれほどスピードを積めばいいのか、

適性◎はスピード70と固定し、
適性〇のスピードを調整してその差を図る。

調査方法は
適性◎を9頭、適性〇を9頭用意し
合計18頭に東京芝2000ｍ（良）を
各スピード差で20回ずつ走ってもらう。

集計したものが以下の通り。

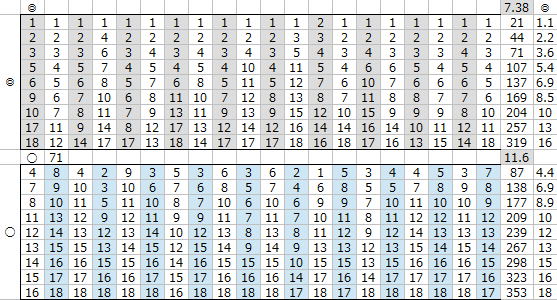
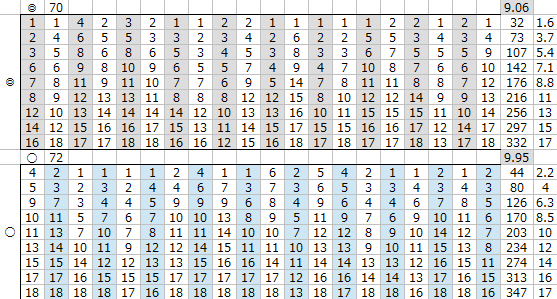
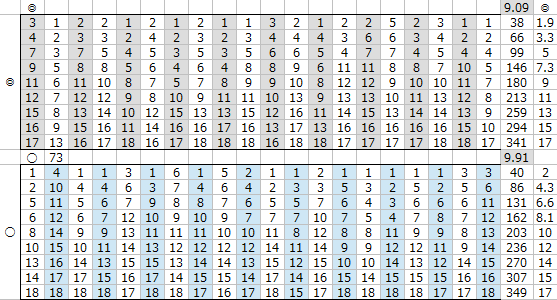
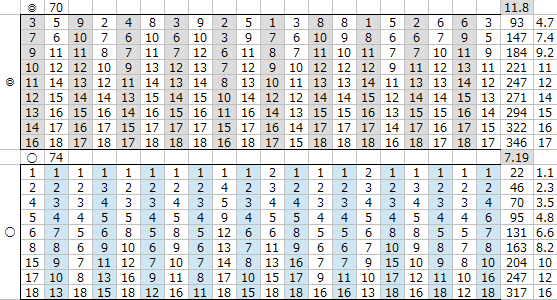
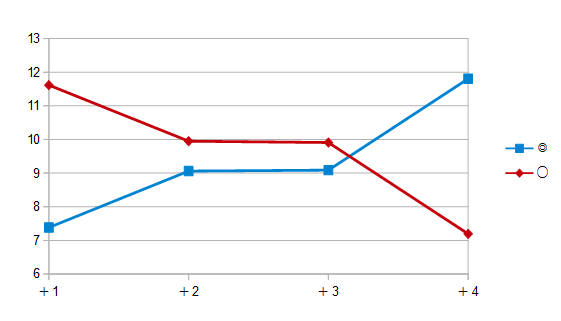
スピード差が+1程度であれば
まだまだ適性◎と同等とは言えないが、

スピード差が+2～3程度となるといい勝負になっている。

スピード差が+4となると適性〇のほうが平均着順の点で適性◎に圧勝しているため、

○と△のスピード差

上と同じように
適性〇をスピード70固定とし、
適性△のスピードを調整して二つの適性差を調査する。

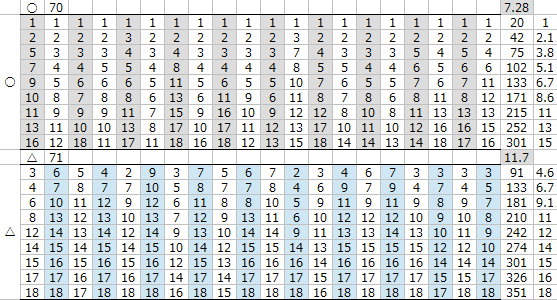
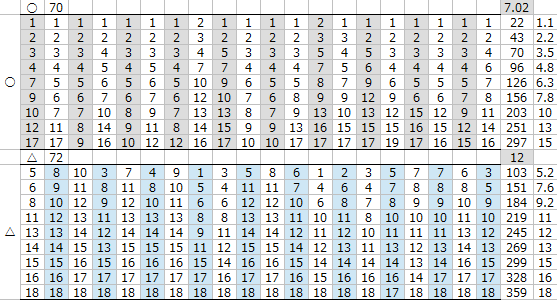
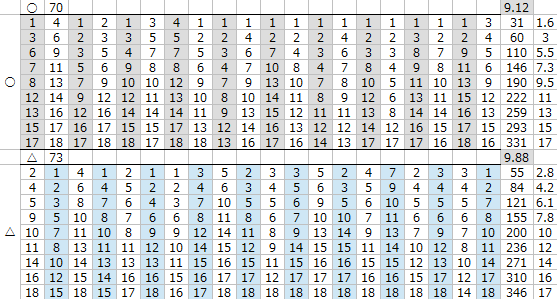
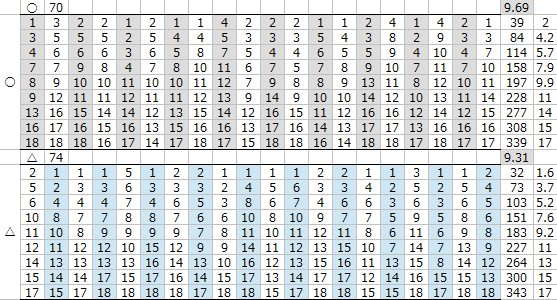
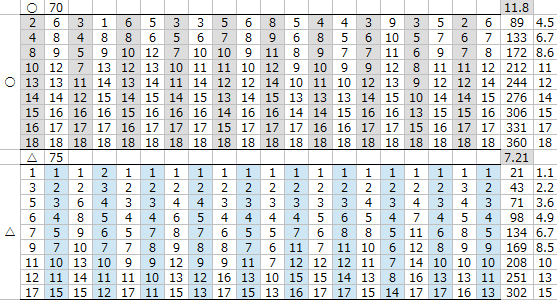
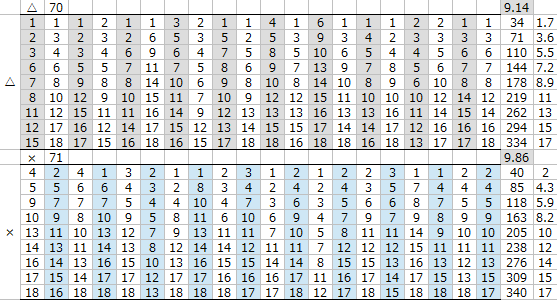
適性〇と△の差は
△のスピードを+2追加する程度では賄いきれず

勝負するにはスピードを+3追加したいところである。

△のスピードを+4加算したところで
全体の平均着順が適性△のほうが良くなり、

スピード+5加算すると
適性△は適性〇を大きく上回る結果となった。

△と×のスピード差

上と同じように
適性△をスピード70固定とし、
適性×のスピードを調整して二つの適性差を調査する。

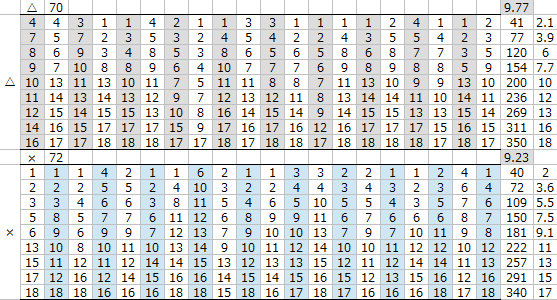
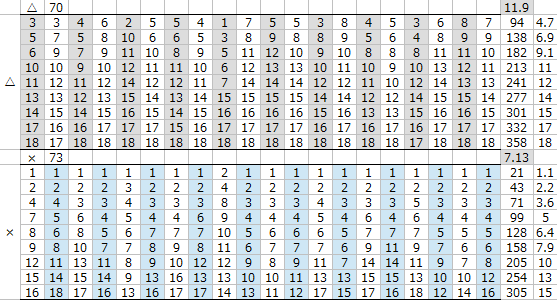
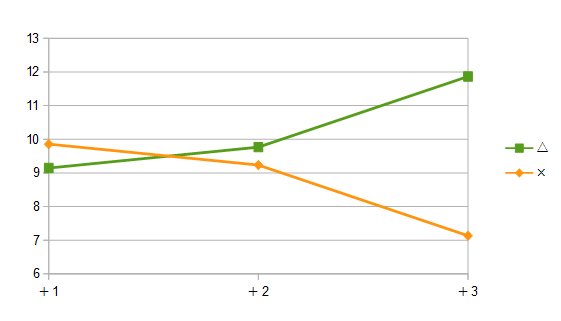
適性△と適性×は
スピードを+1加算した段階で善戦しており、

スピードを+2加算すると
適性×が適性△より全体の平均着順が
僅かながら良くなっていた。

スピードを+3加算すると
適性×が大きくリードしていることから

レースで勝つための適性

以上のことから
各適性の差をスピードのみで埋めるには

ある程度勝負できるようにするために
それほどのスピード差で挑まなければならない。

単純計算で適性△が◎に挑む場合
スピードは+7前後高い状態でなければならないため
これはあまり実用的な数字ではない。

そのため

適性◎が多いレースに挑むには
最低でも適性〇でなければ相手にならない可能性が高くなり、

もちろんスピード差が少ない状態の馬場適性〇であっても
適性◎相手に１着を取ることもあるが、

スピード差が１の馬場適性◎と○の
着順ごとの平均着順は以下の通りであり、
適性◎と比較して適性〇の平均着順は大きく上に振れている。

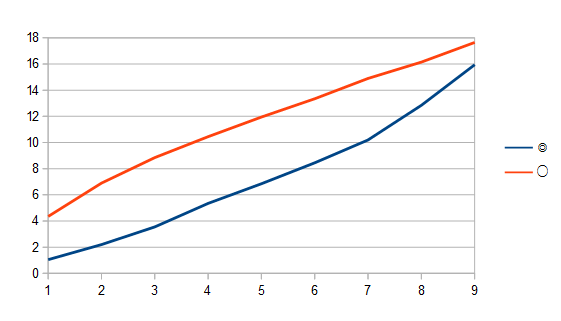
このグラフから
適性◎（青）の入着順上位３頭は全体の４着以内に入ることや
全体の１０着以内に適性〇（赤）が４頭も入らず、適性◎の競走馬が７頭近く入ることがわかる。

さすがにこの状況で
適性◎と○が同等の勝負ができるとは言い難い。

しかし適性〇のスピードを+3加算すると以下の通りとなり、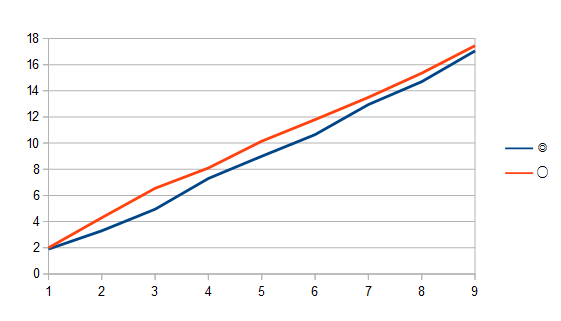

適性◎（青）と適性〇（赤）がほぼ同等となる。

再度申し上げるが
適性〇でスピードは同じであっても
適性◎相手に１着を獲ることは可能である。

kamioka

XYouTube